测试训练-network_based_nearest_neighbors-PROSAGA-码农传奇

Network based Nearest Neighbor Indexer

최인접이웃 (k-nearest neighbors) 는 classification 이나 regression 을 위해 이용되는 non-parametric model 중 하나입니다. Query point 에 대하여 k 개의 가장 가까운 이웃을 찾은 뒤, 그 이웃의 labels 중 가장 많은 label 을 classification 의 predicted label 로 이용하거나, 그 이웃의 y 값의 평균을 regression value 로 이용할 수 있습니다. 그리고 그 이웃간의 거리를 classification 이나 regression 의 weight 로 이용할 수도 있습니다.

그러나 최인접이웃 모델은 query point 가 주어졌을 때, reference data 에서 가까운 이웃들을 찾는 비용이 비쌉니다.

이를 해결하기 위한 다양한 방법이 제안되었습니다. Hash function 기반으로 작동하는 Locality Sensitive Hashing (LSH) 는 가장 대표적인 인덱서입니다. 그러나 이 인덱서는 정확한 k-nearest neighbors 를 찾는다는 보장은 할 수 없습니다 (오류의 범위나 확률은 보장할 수 있습니다). 이처럼 정확하지는 않지만 빠르게 (거의) 최인접인 이웃들을 찾는 방법을 Approximated Nearest Neighbor Search (ANNS) 라 합니다.

Hash function 을 이용하는 방법들 외에도 network 를 이용하는 방법이 있습니다.

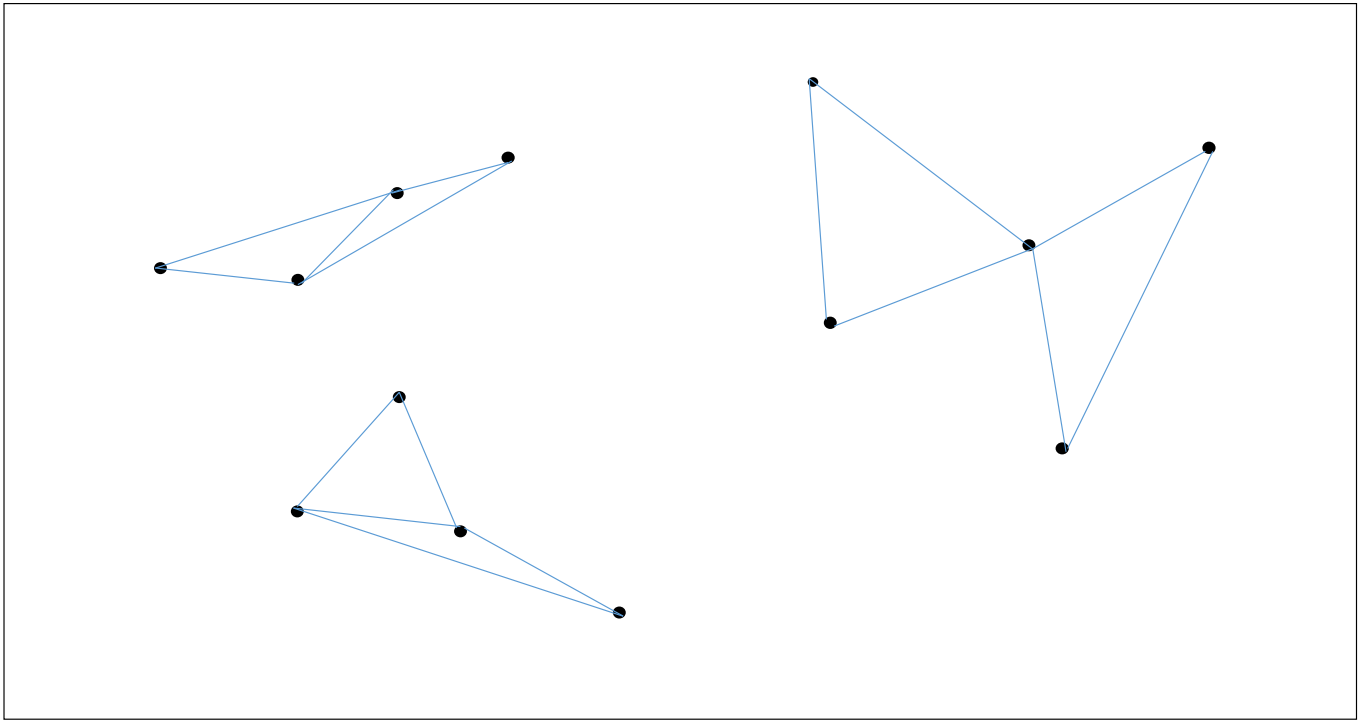
아래 그림은 원리 설명을 위한 예시 데이터입니다. 13 개의 2 차원의 데이터입니다.

각 점마다 가장 가까운 2 개의 점들을 이어줍니다. 반드시 모든 점의 이웃의 갯수가 같을 필요는 없습니다. 작은 숫자이면 됩니다. 또한 단방향, 양방향이어도 상관없습니다. 자신과 가까운 점들을 알고 있는 것이 중요합니다.

여기서 한 가지, 우리가 풀려 하는 문제는 주어진 reference data 에 대하여 가장 가까운 점들을 빠르게 찾는 것이 아닙니다. 임의의 query point 에 대하여 빠르게 k-nearest neighbors 를 찾는 것입니다. Reference data 에 대한 k-nearest neighbor graph 를 만드는 것은 한 번의 training 입니다. Querying time 을 빠르게 만드는 것이 목표입니다.

물론 이 과정에서 NN-Descent 와 같은 neighbor graph 를 빠르게 만들어주는 알고리즘을 이용할 수도 있습니다.

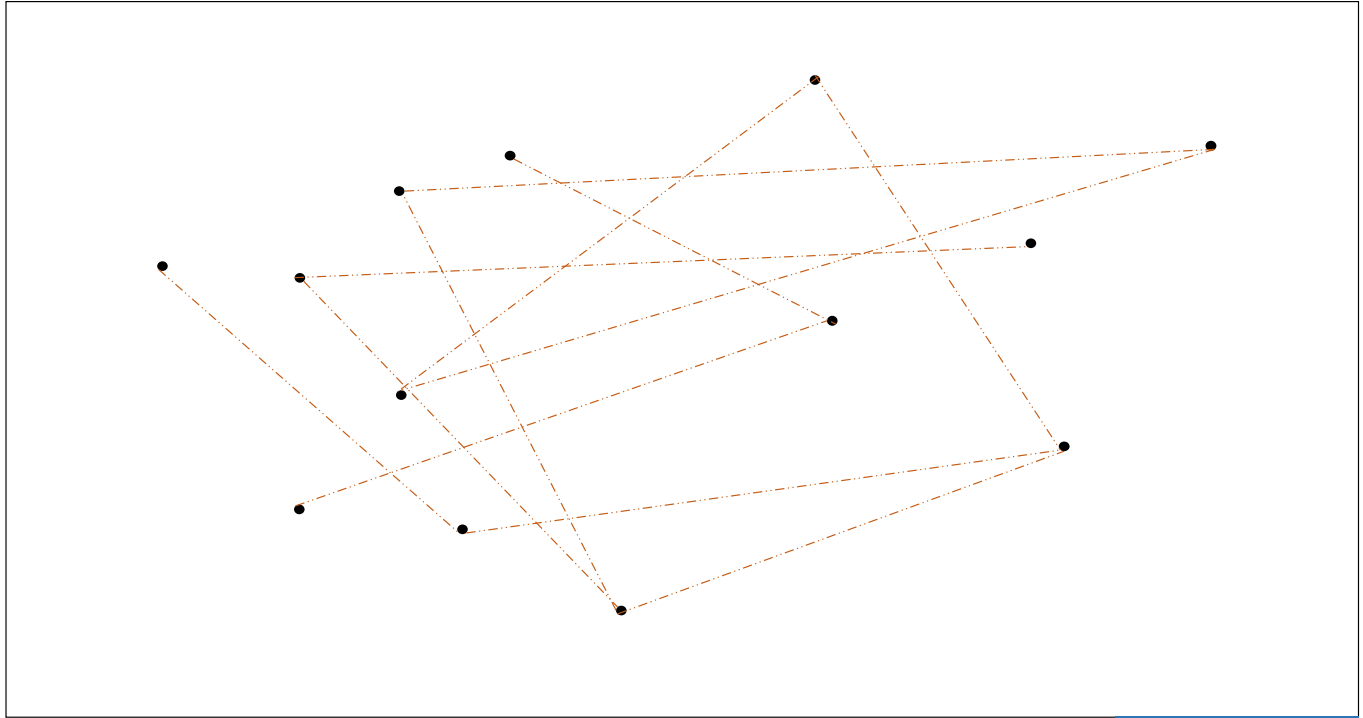
두번째로, 각 점 마다 임의로 몇 개의 점을 연결합니다. Random connected graph 입니다. 이는 한 지역에서 다른 지역으로 jump 를 할 수 있는, 일종의 고속도로 역할을 합니다.

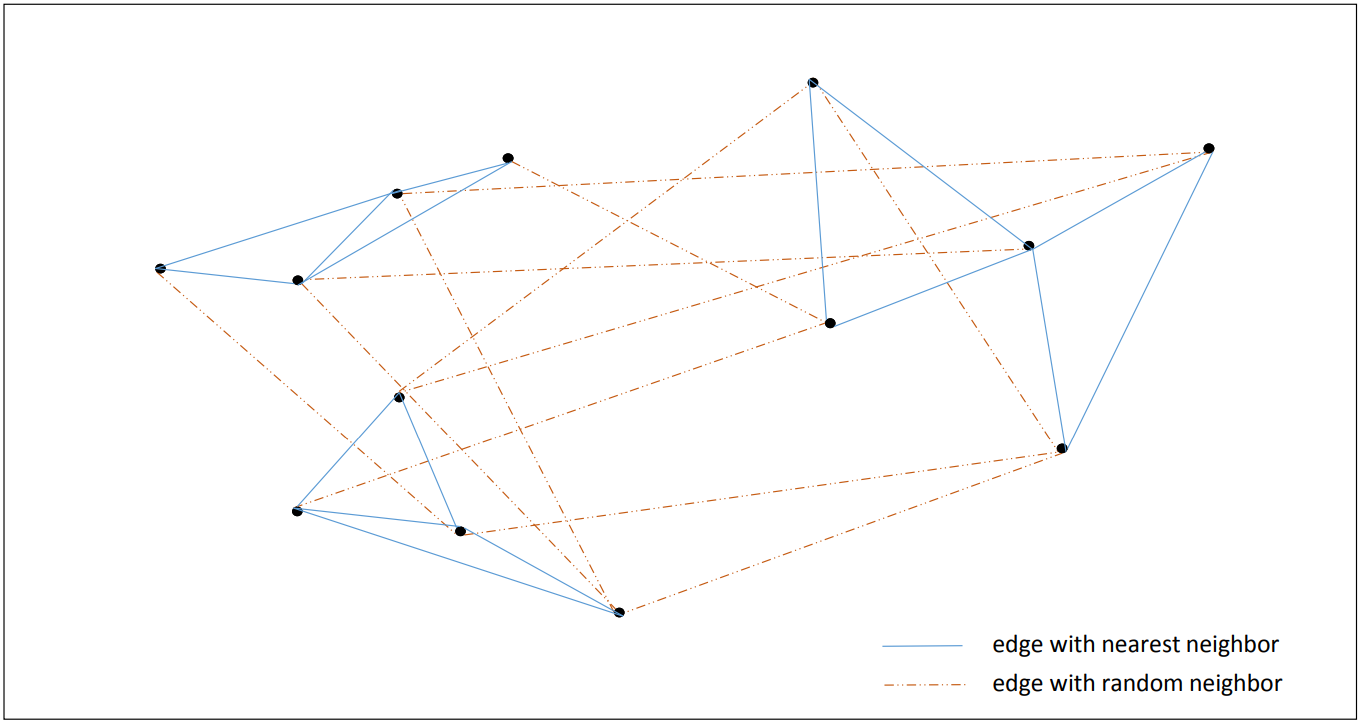
그리고 이 두 그래프 (nearest neighbor, random neighbor graph) 를 겹쳐줍니다. 이 과정까지가 indexing 입니다.

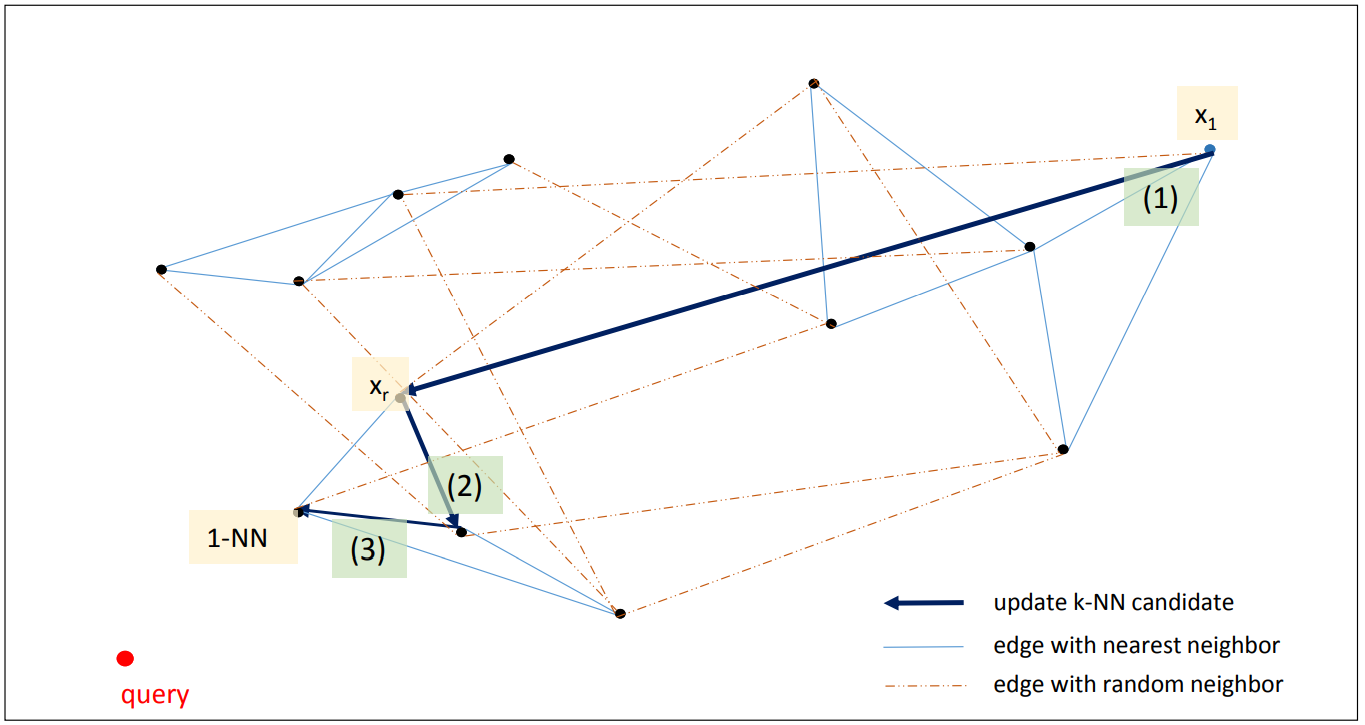
초기화: 하나의 query point 가 주어지면 p 개의 임의의 seed points 를 선택합니다. 아래 그림에서는 하나의 점 x1 을 선택하였습니다. x1 에서 이동할 수 있는 점 (nearest & random neighbor of x1) 중에서 query point 와 더 가까운 p 개의 점을 선택합니다 (아래 그림에서는 p=1 입니다).

반복 탐색: 임의로 선택하였기 때문에 query point 와 매우 먼 x1 이 선택되었고, nearest neighbor of x1 중에서는 query point 와 가까운 점이 없습니다. 대신 random neighbors 중에서 query point 와 가까운 xr 이 있습니다. 이 점을 frontier points 로 설정합니다. 현재까지 알려진 query point 와 가장 가까운 p 개의 점이라는 의미입니다. 이 점의 nearest & random neighbors 중에서 query point 와 가까운 점은 없는지 다시 탐색합니다. 점점 query point 와 가까운 점으로 frontier points 가 업데이트 됩니다.

반복 탐색 종료: 이 과정을 미리 설정된 max steps 번 만큼 반복하던지, frontier points 가 변하지 않을 때까지만 반복합니다.

p 는 k 이상이면 됩니다. 오히려 찾아야 하는 nearest neighbors 의 개수인 k 보다 더 큰 p 개의 frontier points 를 유지하는 것이 탐색을 더 빠르게 만들어줍니다.

Usage

Indexing

from network_based_nearest_neighbors import NetworkBasedNeighbors
index = NetworkBasedNeighbors(
    X,                     # reference data. numpy.ndarray or scipy.sparse.csr_matrix
    n_nearest_neighbors=5, # number of nearest neighbors
    n_random_neighbors=5,  # number of random neighbors
    batch_size=500,        # indexing batch size
    metric='euclidean',    # metric, possible all metric defined in scipy
    verbose=True           # verbose mode if True
)

Querying

k = 10
index.search_neighbors(query, k=k) # query: a row vector

TODO

현재 indexing 시간이 오래 걸리는 이유는 nearest neighbor graph 를 만들기 위하여 brute-force 로 모든 pairwise distance 를 계산하기 때문입니다. 이 부분은 NN-descent 와 같은 더 빠른 nearest neighbor graph constructor 로 대체해야 합니다.

이 알고리즘의 작동 원리 및 구현 과정에 대한 내용을 블로그 포스트에 적어두었습니다.

Network based Nearest Neighbor Indexer

Usage

TODO

Read more